2-convex-set

Convex Set

Given \(x^1, \dots, x^k \in \R^n\), we say that \(y = \sum_{i=1}^k \alpha_i x^{i}\) is

• a linear combination of \(x^1, \dots, x^k\) if \(\alpha_1, \dots, \alpha_k \in \R\);
• an affine combination of \(x^1, \dots, x^k\) if \(\sum_{i=1}^k \alpha_i = 1\);
• a convex combination of \(x^1, \dots, x^k\) if \(\sum_{i=1}^k \alpha_i = 1\) and \(0 \le \alpha_1, \dots, \alpha_k\).

Let \(S \in \R^n\),

• \(S\) is a linear subspace if \(\forall x,y \in S, \alpha,\beta \in \R, \alpha x + \beta y \in S\);
• \(S\) is an affine subspace if \(\forall x,y \in S, \alpha \in \R, \alpha x + (1-\alpha) y \in S\);
• \(S\) is a convex set if \(\forall x,y \in S, 0 \le \alpha \le 1, \alpha x + (1 - \alpha) y \in S\).

Proposition: The following statements are equivalent:

• \(S\) is affine.
• Any affine combination of a finite number of points in \(S\) belongs to \(S\).
• \(S\) can be written as \(S = {x} + V \triangleq \{ x + v: v \in V \}\). Note that though \(V\) is unique, \(x\) is not.

Proposition: The following statements are equivalent:

• \(S\) is convex.
• Any convex combination of a finite number of points in \(S\) belongs to \(S\).

Examples of Convex Set

1. Nonnegative orthant (in 2-D, an orthant is called a quadrant): \(\R^n_+ \triangleq \{ x \in \R^n: \forall i, x_i \ge 0 \}\)

2. Hyperplane

   Given \(w \in \R^n, b \in R\), the hyperplane \(H(s, c)\) is the set \(\{ x \in \R^n: s^T x = c \}\)

3. Half-space

   Given \(w \in \R^n, b \in R\), the upper half-space \(H^+(s, c)\) is the set \(\{ x \in \R^n: s^T x \ge c \}\); the lower half-space \(H^-(s, c)\) is the set \(\{ x \in \R^n | s^T x \le c \}\).

   Note that hyperplane \(H(s, c)\) is the intersection of \(H^+(s, c)\) and \(H^-(s, c)\).

4. Euclidean ball

   Given the center \(\bar x \in \R^n\) and the radius \(r > 0\), the Euclidean ball \(B(\bar x, r)\) is the set \(\{ x \in \R^n: ||x - \bar x||_2 \le r \}\).

   A generalization of Euclidean ball would be to extend the norm to other numbers that are larger than 1. For \(q \ge 1\) \[ B_q(\bar x, r) = \{ x \in \R^n: ||x - \bar x||_q \le r \} \] is also a convex set. Note that \(||z||_\infty = \lim_{q \to \infty} (\sum_i z_i^q)^{1/q} = \max_i z_i\).

5. Convex cone

   Definition: A set \(K \in \R^n\) is called a cone if \(\forall x \in K, \alpha > 0, \alpha x \in K\).

   Linear subspace is a cone. Affine subspace is not necessarily so.

   Definition: A convex cone is a cone that is convex.

   Some examples of convex cone include \(\R^n_+\), and \(\mathcal{S}_+^n\), which is the set of \(n \times n\) PSD matrices.

Convexity-preserving Operations

For any two convex sets \(S_1\) and \(S_2\), there are some binary operators that will preserve the convexity after being applied.

1. Set operations

   \(S_1 \cup S_2\) is not necessarily convex. \(S_1 \cap S_2\) is always convex.

2. Affine transformations

   Definition: We say that \(A: \R^n \mapsto \R^m\) is affine if \(\forall x,y \in \R^n, \alpha \in \R\), \[ A(\alpha x + (1 - \alpha) y) = \alpha A(x) + (1 - \alpha) A(y) \]

   Let \(A: \R^n \mapsto \R^m\) be affine, \(S \subseteq \R^n\) be convex. Then \(A(S) \triangleq \{ A(x): x \in S \}\) is convex.

   There are two types of affine transformation worth noting.

   • Rotation: \(A(x) = U x\) where \(U \in \R^{n \times n}\) and \(U U^T = U^T U= I\).

   • Projection: \(A(x) = P x\) where \(P \in \R^{n \times n}\) and \(P^2 = P\).

     For orthogonal projection, its projection matrix further satisfies \(P^T = P\).

   As an example of affine transformation, given center \(\bar x\) and axes \(Q\) which is positive definite, the ellipsoid \(E(\bar x, Q)\) is the set \(\{ x \in \R^n | (x - \bar x)^T Q (x - \bar x) \le 1 \}\). Note that \(B(\bar x, r) = E(\bar x, I/r^2)\).

   Remark: When \(Q\) is positive semi-definite, it might occur that \(\{ x \in \R^n | (x - \bar x)^T Q (x - \bar x) \le 1 \}\) will degenerate into two parallel lines. Just consider the case when \(Q = [1,2] [1,2]^T\).

   Proposition: There always exists an affine transformation \(A: \R^n \mapsto \R^n\) such that \(A(B(0, 1)) = E(\bar x, Q)\). Note that \(B(\bar x, r) = E(\bar x, I/r^2)\). See this handout for the construction of such transformation.

   Therefore, ellipsoid is also a convex set (Problem 2 of Homework 1 proves this from the first principle).

Topological Preparation

Basic Topology

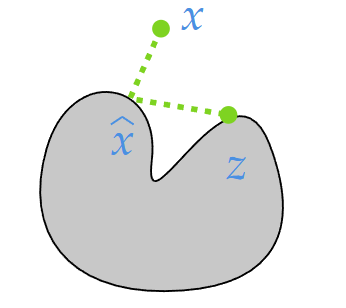
Definition: Given a set \(S \in \R^n, S \ne \emptyset\) and a point \(x \notin S\), we want to find a point in \(S\) that is closest (in terms of Euclidean distance) to \(x\). Formally, \(\hat x = \arg\min_{z \in S} ||z - x||_2\) is called the projection of \(x\) onto \(S\), denoted as \(\hat x = \Pi_S(x)\).

Note that this projection does not necessarily exist. Neither the projection is unique. Under what conditions can we guarantee the existence and uniqueness of projection? Before that, some concepts are needed. Let \(S \subseteq \R^n\) be a set.

Definition: \(x\) is an interior point of \(S\) if \(\exists \epsilon > 0, B(x, \epsilon) \subseteq S\). The collection of all interior points of \(S\) is called the interior of \(S\), denoted as \(\mathop{\mathrm{int}} S\).

We say that \(S\) is open if \(S = \mathop{\mathrm{int}} S\). We say that \(S\) is closed if \(\R^n \setminus S\) is open. Note that it can be the case that a set is neither open nor closed.

Proposition: The intersection of any family of closed sets is closed.

Proposition: Let \(f: \R^n \mapsto \R\) be continuous and \(c \in \R\) be a constant number. Then \(S = \{ x \in \R^n: f(x) \le c \}\) is closed.

Proposition: \(S\) is closed if and only if for every convergent sequence \(\{ x_n \}\) in \(S\), its limit is in \(S\).

Definition: We say that \(S \subseteq \R^n\) is compact if it is closed and bounded (\(\exists M > 0\) such that \(S \subseteq B(0, M)\)).

Projection

Weierstrass theorem: Let \(f: \R^n \mapsto \R\) be continuous and \(S \subseteq \R^n\) be compact. Then \(\inf_{x \in S} f(x)\) always has a solution.

Theorem: Let \(S \subseteq \R^n\) be non-empty, closed, and convex. Then for every \(x \in \R^n\), there exists a unique \(\hat x\) such that \(\hat x = \Pi_S(x)\).

Proof:

• Existence

  We may assume that \(x \notin S\). Consider any \(x' \in S\) and define \(T \triangleq S \cap B(x, ||x - x'||_2)\). Observe that

  1. \(\arg \min_{z \in S} ||x - z||_2 = \arg \min_{z \in T} ||x - z||_2\).
  2. \(T\) is closed and bounded.

  Then by Weierstrass’ theorem, \(\hat x\) that solves \(\min_{z \in T} ||x - z||_2\) exists. And by Point 1 above, \(\hat x = \Pi_S(x)\). Note that above argument does not need convexity.

• Uniqueness

  Suppose on the contrary that \(\hat x_1 = \Pi_S(x), \hat x_2 = \Pi_S(x)\) and \(\hat x_1 \ne \hat x_2\). Let \(z = (\hat x_1 + \hat x_2) / 2\). By convexity, \(z \in S\). Then \(x\)’s distance to \(z\) can be calculated as \[ \begin{aligned} || x - (\hat x_1 + \hat x_2)/2 ||_2 &= || (x - \hat x_1)/2 + (x - \hat x_2)/2 ||_2 \\ &\le || (x - \hat x_1)/2 ||_2 + || (x - \hat x_2)/2 ||_2 \\ &= \min_{z \in S} ||x - z||_2 \end{aligned} \] If the \(\le\) is strict, the fact that \(\hat x_1\) and \(\hat x_2\) are the projection will be contradicted; else \((x - \hat x_1)\) and \((x - \hat x_2)\) are collinear, which means \(x, \hat x_1, \hat x_2\) are collinear, in which case the only possible way for \((x - \hat x_1)\) and \((x - \hat x_2)\) to be equal is \(\hat x_1 = \hat x_2\), contradicting the assumption \(\hat x_1 \ne \hat x_2\).

  As a result, \(\hat x_1 = \hat x_2\), which means the projection of \(x\) is unique.

Theorem: Let \(S \subseteq \R^n\) be non-empty, closed, and convex. Then for any \(x \in \R^n\), we have \[ \hat x = \Pi_{S}(x) \iff \forall z \in S, (z - \hat x)^T(x - \hat x) \le 0 \] Proof:

• Necessity

  For any \(z \in S\) and \(0 \le \alpha \le 1\), define \(z(\alpha) = \alpha z + (1 - \alpha) \hat x\). By convexity, \(z(\alpha) \in S\). Then, \[ ||\hat x - x||_2^2 \le ||z(\alpha) - x||_2^2 \] Note on the other hand that \[ \begin{aligned} &\quad ||z(\alpha) - x||_2^2 = [z(\alpha) - x]^T [z(\alpha) - x] \\ &= [\hat x + \alpha (z - \hat x) - x]^T [\hat x + \alpha (z - \hat x) - x] \\ &= [(\hat x - x) + \alpha (z - \hat x)]^T [(\hat x - x) + \alpha (z - \hat x)] \\ &= ||\hat x - x||_2^2 + 2\alpha (z - \hat x)^T (\hat x - x) + \alpha^2 ||z - \hat x||_2^2 \end{aligned} \] To make the above hold for any \(\alpha \in [0,1]\), it must be the case that \((z - \hat x)^T (\hat x - x) \ge 0\) or equivalently \[ (z - \hat x)^T (x - \hat x) \le 0 \] Convexity is crucial in this property. Just consider the following case:

  

• Sufficiency

  Suppose on the contrary that there exists some \(x' \ne \Pi_S(x)\) such that for every \(z \in S\), \[ (z - x')^T (x - x') \le 0 \] Then for \(\Pi_S(x) \in S\), we have \[ \begin{equation} (\Pi_S(x) - x')^T (x - x') \le 0 \label{eq1} \end{equation} \] From the proof of sufficiency we know that for this specific \(x'\), \[ \begin{equation} (x' - \Pi_S(x))^T (x - \Pi_S(x)) \le 0 \label{eq2} \end{equation} \] Add up together \(\eqref{eq1}\) and \(\eqref{eq2}\) to give \[ (\Pi_S(x) - x')^T (\Pi_S(x) - x') \le 0 \] This indicates that \(\Pi_S(x) = x'\), which concludes the proof.

Separation

Given \(S_1, S_2 \subseteq \R^n\), it is easy to certify that \(S_1 \cap S_2 \ne \emptyset\) so long as there is a \(x \in S_1\) such that \(x \in S_2\). But how can one certify that \(S_1 \cap S_2 = \emptyset\)?

One geometric intuition is to find a hyperplane \(H(s,c)\) such that \(S_1 \subseteq H^+(s,c) \setminus H(s,c)\) and \(S_2 \subseteq H^-(s,c) \setminus H(s,c)\). Obviously a hyperplane separation won’t always work. But it helps in the discussion of convex set.

Theorem: point-set separation. Let \(S \subseteq \R^n\) be non-empty, closed and convex. Let \(x \notin S\). Then there exists \(y \in \R^n\) such that \[ \left( \max_{z \in S} y^T z \right) < y^T x \] Proof:

By the projection theorem, \(\hat x \triangleq \Pi_S(x)\) exists and is unique. Take \(y\) as \((x - \hat x)\). \(y \ne \vec 0\) because \(x \notin S\). Then according the projection’s property, for every \(z \in S\), \[ \begin{gather} \begin{aligned} (z - \hat x)^T \underbrace{(x - \hat x)}_{y} &\le 0 \\ z^T y - \hat x^T y &\le 0 \\ \end{aligned} \quad \Rightarrow \quad \begin{aligned} y^T z &\le y^T (x - y) \\ &\le y^T x - ||y||_2^2 \\ &< y^T x \end{aligned} \end{gather} \] \(\max_{z \in S} y^T z\) is obtained at \(z = \hat x\), which concludes the proof.

The theorem above is an algebraic description of point-set separation and in essence reveals a hyperplane separation. \(y\) is exactly the normal vector of this hyperplane. \((\max_{z \in S} y^T z) < y^T x\) actually says that \(x\) is more distant in the direction of \(y\) than every point \(z\) in \(S\).

A direct result of the theorem above is that

Theorem: A closed convex set \(S \subseteq \R^n\) is the intersection of all half-spaces containing \(S\), i.e. \[ S = \bigcap_{\substack{\text{$S \subseteq H$ and} \\ \text{$H$ is a halfspace}}} H \] Proof:

Without loss of generality, due to that \(H^+(s,c) = H^-(-s,-c)\), we claim that \(S\) is the intersection of all the lower half-spaces containing \(S\): \[ S = \bigcap_{H^-(s, c) \supseteq S} H^-(s,c) \] We begin with two special cases: \(\emptyset\) and \(\R^n\). We show that \(\emptyset\) and \(\R^n\) satisfies the above because \[ \emptyset = H^-(0, -1) \cap \text{any lower halfspace} \\ \R^n = \bigcap_{c \ge 0} H^-(0, c) \] Now consider any set \(\emptyset \subsetneq S \subsetneq \R^n\). Let \(x \notin S\). Then by point-set separation theorem, there exists \(y_x \in \R^n\) such that \[ c_x \triangleq \max_{z \in S} y_x^T z < y_x^T x \] Therefore, \(S \subseteq H^-_x \triangleq H^-(y_x, c_x)\). Note that \(x \notin H^-_x\). \(S \subseteq H^-_x\) holds for any \(x \notin S\). Therefore, \[ S \subseteq \bigcap_{x \notin S} H^-_x \] On the other hand, \(\bigcap_{x \notin S} H^-_x \subseteq S\). Suppose on the contrary there exists \(z \in \bigcap_{x \notin S} H^-_x\) but \(z \notin S\). However, \[ z \in \bigcap_{x \notin S} H^-_x = \bigcap_{\{ x \notin S: x \ne z \} \cup \{ z \} } H^-_x \subseteq H^-_z \] which contradicts the fact that \(z \notin H^-_z\). Therefore, \(\bigcap_{x \notin S} H^-_x \subseteq S\) and consequently \[ S = \bigcap_{x \notin S} H^-_x \] Notice that \(\{ H^-_x: x \notin S \}\) contains all the lower half-spaces that superset \(S\). Because for every lower half-space \(H^-(s, c) \supseteq S\), there exists \(x \in H^+(s, c) \setminus H(s, c)\) such that \(x \notin S\). For this specific \(x\), there exists \(s\) such that \[ \max_{z \in S} s^T z \le c < s^T x \] Therefore, every \(H^-(s, c) \supseteq S\) can be written as \(H^-_x\) for some \(x \notin S\), which concludes the proof.

By far, the separation between a point (or a set of a single point) and a set is settled. Now we consider the set-set separation. It is easy to conjecture the geometric intuition derived above as the following:

Conjecture: set-set separation. Let \(S_1, S_2 \subseteq \R^n\) be two non-empty, closed and convex sets with \(S_1 \cap S_2 = \emptyset\). Then there exists \(y \in \R^n\) such that \[ \max_{z \in S_1} y^T z < \min_{z \in S_2} y^T z \] Disproof:

Just consider \(S_1 = \{ (u, v): u \ge 1/v, v \ge 1 \}\) and \(S_2 = \{ (u, 0): u \ge 1 \}\). The only possible separation hyperplane is the \(x\)-axis, with the corresponding normal vector \(y = [0, -1]^T\). However in this case, \(\max_{z \in S_1} y^T z\) does not exist at all and thus \(\max_{z \in S_1} y^T z < \min_{z \in S_2} y^T z\) does not hold.

Trivially changing \(\max\) to \(\sup\) won’t help, since \(\sup_{z \in S_1} [0, -1] z = 0\).

Lack of boundedness forbids us to take the advantage of Weierstrass’ theorem to show the existence of maxima. It would be cheering if the predicate of the conjecture can be relaxed so that boundedness and thus compactness applies, yielding the following:

Theorem: set-set separation. Let \(S_1, S_2 \subseteq \R^n\) be two non-empty, closed and convex sets, with \(S_1 \cap S_2 = \emptyset\) and either \(S_1\) or \(S_2\) being bounded. Then there exists \(y \in \R^n\) such that \[ \max_{z \in S_1} y^T z < \min_{z \in S_2} y^T z \] Hint of proof:

We only show the proof when \(S_2\) is bounded. The case when \(S_1\) is bounded can be handled similarly.

Consider the set \(S \triangleq \{ x - y: x \in S_1, y \in S_2 \}\) (which will be \(\{ x - y: x \in S_2, y \in S_1 \}\) in the other case). Since \(S_1 \cap S_2 = \emptyset\), \(0 \notin S\). \(S\) is non-empty obviously. \(S\) can be further verified to be closed and convex (??). Then the property of point-set separation can be applied to proceed with the proof.

That is, there exists \(u \in \R^n\) such that \[ \left( \max_{z \in S} u^T z \right) < u^T \cdot 0 = 0 \\ \Downarrow \\ \max_{x \in S_1, y \in S_2} u^T (x - y) < 0 \]

Set \(y\) as \(y^* = \min_{y \in S_2} u^T y\) (such \(y^*\) exists because the compactness of \(S_2\)) to give \[ \begin{aligned} \max_{x \in S_1} u^T (x - y^*) &< 0 \\ \max_{x \in S_1} u^T x &< u^T y^* \\ \max_{x \in S_1} u^T x &< \min_{y \in S_2} u^T y \\ \end{aligned} \] which concludes the proof.

For a richer discussion of convex set separation, please refer here.